
Custom Search
ZEROTH LAW OF THERMODYNAMICS
_
The zeroth law of thermodynamics is a generalization principle of thermal equilibrium among bodies, or thermodynamic systems, in contact.
The zeroth law states that if two systems are in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.
Systems are said to be in thermal equilibrium if they are able to transfer heat between each other (for example by conduction or radiation) but do not do so. Systems can also be said to be in thermal equilibrium if they are not able to transfer heat to each other, but would not do so if able. The law implies that thermal equilibrium between systems is a transitive relation, which affords the definition of an empirical physical parameter, called temperature. The temperatures are equal for all systems in thermal equilibrium. The law permits the construction of a thermometer to measure this property.
The zeroth law of thermodynamics is a generalization principle of thermal equilibrium among bodies, or thermodynamic systems, in contact.
The zeroth law states that if two systems are in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.
Systems are said to be in thermal equilibrium if they are able to transfer heat between each other (for example by conduction or radiation) but do not do so. Systems can also be said to be in thermal equilibrium if they are not able to transfer heat to each other, but would not do so if able. The law implies that thermal equilibrium between systems is a transitive relation, which affords the definition of an empirical physical parameter, called temperature. The temperatures are equal for all systems in thermal equilibrium. The law permits the construction of a thermometer to measure this property.
ZEROTH LAW AS EQUIVALENCE RELATION
_
A system is said to be in thermal equilibrium when it experiences no net change in thermal energy. If A, B, and C are distinct thermodynamic systems, the zeroth law of thermodynamics can be expressed as:
"If A and C are each in thermal equilibrium with B, A is also in equilibrium with C."
This statement asserts that thermal equilibrium is a Euclidean relation between thermodynamic systems. If we also grant that all thermodynamic systems are in thermal equilibrium with themselves, then thermal equilibrium is also a reflexive relation. Relations that are both reflexive and Euclidean are equivalence relations. One consequence of this reasoning is that thermal equilibrium is a transitive relationship: If A is in thermal equilibrium with B and B is in thermal equilibrium with C, then A is in thermal equilibrium with C. Another consequence is that the equilibrium relationship is symmetric: If A is in thermal equilibrium with B, then B is in thermal equilibrium with A. Thus we may say that two systems are in thermal equilibrium with each other, or that they are in mutual equilibrium. Implicitly assuming both reflexivity and symmetry, the zeroth law is therefore often expressed as
"If two systems are in thermal equilibrium with a third system, then they are in thermal equilibrium with each other"
Again, implicitly assuming both reflexivity and symmetry, the zeroth law is occasionally expressed as the transitive relationship
"If A is in thermal equilibrium with B and if B is in thermal equilibrium with C, then A is in thermal equilibrium with C."
A system is said to be in thermal equilibrium when it experiences no net change in thermal energy. If A, B, and C are distinct thermodynamic systems, the zeroth law of thermodynamics can be expressed as:
"If A and C are each in thermal equilibrium with B, A is also in equilibrium with C."
This statement asserts that thermal equilibrium is a Euclidean relation between thermodynamic systems. If we also grant that all thermodynamic systems are in thermal equilibrium with themselves, then thermal equilibrium is also a reflexive relation. Relations that are both reflexive and Euclidean are equivalence relations. One consequence of this reasoning is that thermal equilibrium is a transitive relationship: If A is in thermal equilibrium with B and B is in thermal equilibrium with C, then A is in thermal equilibrium with C. Another consequence is that the equilibrium relationship is symmetric: If A is in thermal equilibrium with B, then B is in thermal equilibrium with A. Thus we may say that two systems are in thermal equilibrium with each other, or that they are in mutual equilibrium. Implicitly assuming both reflexivity and symmetry, the zeroth law is therefore often expressed as
"If two systems are in thermal equilibrium with a third system, then they are in thermal equilibrium with each other"
Again, implicitly assuming both reflexivity and symmetry, the zeroth law is occasionally expressed as the transitive relationship
"If A is in thermal equilibrium with B and if B is in thermal equilibrium with C, then A is in thermal equilibrium with C."
THERMAL EQUILIBRIUM BETWEEN MANY STATES
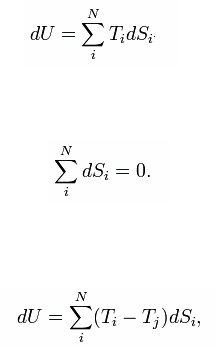
_
Many systems are said to be in equilibrium if the small, random exchanges (due to Brownian motion or photon emissions, for example) between them do not lead to a net change in the total energy summed over all systems. A simple example illustrates why the zeroth law is necessary to complete the equilibrium description.
Consider N systems in adiabatic isolation from the rest of the universe, i.e. no heat exchange is possible outside of these N systems, all of which have a constant volume and composition, and which can only exchange heat with one another.
The combined First and Second Laws relate the fluctuations in total energy, , to the temperature of the ith system, and the entropy fluctuation in the ith system, as follows:
The adiabatic isolation of the system from the remaining universe requires that the total sum of the entropy fluctuations vanishes, or:
That is, entropy can only be exchanged between the N systems. This constraint can be used to rearrange the expression for the total energy fluctuation and obtain:
Many systems are said to be in equilibrium if the small, random exchanges (due to Brownian motion or photon emissions, for example) between them do not lead to a net change in the total energy summed over all systems. A simple example illustrates why the zeroth law is necessary to complete the equilibrium description.
Consider N systems in adiabatic isolation from the rest of the universe, i.e. no heat exchange is possible outside of these N systems, all of which have a constant volume and composition, and which can only exchange heat with one another.
The combined First and Second Laws relate the fluctuations in total energy, , to the temperature of the ith system, and the entropy fluctuation in the ith system, as follows:
The adiabatic isolation of the system from the remaining universe requires that the total sum of the entropy fluctuations vanishes, or:
That is, entropy can only be exchanged between the N systems. This constraint can be used to rearrange the expression for the total energy fluctuation and obtain:
FOUNDATION OF TEMPERATURE
_
The zeroth law establishes thermal equilibrium as an equivalence relationship. An equivalence relationship on a set (such as the set of thermally equilibrated systems) divides that set into a collection of distinct subsets ("disjoint subsets") where any member of the set is a member of one and only one such subset. In the case of the zeroth law, these subsets consist of systems which are in mutual equilibrium. This partitioning allows any member of the subset to be uniquely "tagged" with a label identifying the subset to which it belongs. Although the labeling may be quite arbitrary, temperature is just such a labeling process which uses the real number system for tagging. The zeroth law justifies the use of suitable thermodynamic systems as thermometers to provide such a labeling, which yield any number of possible empirical temperature scales, and justifies the use of the second law of thermodynamics to provide an absolute, or thermodynamic temperature scale. Such temperature scales bring additional continuity and ordering (i.e., "hot" and "cold") properties to the concept of temperature.
In the space of thermodynamic parameters, zones of constant temperature form a surface, that provides a natural order of nearby surfaces. One may therefore construct a global temperature function that provides a continuous ordering of states. The dimensionality of a surface of constant temperature is one less than the number of thermodynamic parameters, thus, for an ideal gas described with three thermodynamic parameters P, V and n, it is a two-dimensional surface.
For example, if two systems of ideal gases are in equilibrium, then P1V1/N1 = P2V2/N2 where Pi is the pressure in the ith system, Vi is the volume, and Ni is the amount (in moles, or simply the number of atoms) of gas.
The surface PV/N = const defines surfaces of equal thermodynamic temperature, and one may label defining T so that PV/N = RT, where R is some constant. These systems can now be used as a thermometer to calibrate other systems. Such systems are known as "ideal gas thermometers".
The zeroth law establishes thermal equilibrium as an equivalence relationship. An equivalence relationship on a set (such as the set of thermally equilibrated systems) divides that set into a collection of distinct subsets ("disjoint subsets") where any member of the set is a member of one and only one such subset. In the case of the zeroth law, these subsets consist of systems which are in mutual equilibrium. This partitioning allows any member of the subset to be uniquely "tagged" with a label identifying the subset to which it belongs. Although the labeling may be quite arbitrary, temperature is just such a labeling process which uses the real number system for tagging. The zeroth law justifies the use of suitable thermodynamic systems as thermometers to provide such a labeling, which yield any number of possible empirical temperature scales, and justifies the use of the second law of thermodynamics to provide an absolute, or thermodynamic temperature scale. Such temperature scales bring additional continuity and ordering (i.e., "hot" and "cold") properties to the concept of temperature.
In the space of thermodynamic parameters, zones of constant temperature form a surface, that provides a natural order of nearby surfaces. One may therefore construct a global temperature function that provides a continuous ordering of states. The dimensionality of a surface of constant temperature is one less than the number of thermodynamic parameters, thus, for an ideal gas described with three thermodynamic parameters P, V and n, it is a two-dimensional surface.
For example, if two systems of ideal gases are in equilibrium, then P1V1/N1 = P2V2/N2 where Pi is the pressure in the ith system, Vi is the volume, and Ni is the amount (in moles, or simply the number of atoms) of gas.
The surface PV/N = const defines surfaces of equal thermodynamic temperature, and one may label defining T so that PV/N = RT, where R is some constant. These systems can now be used as a thermometer to calibrate other systems. Such systems are known as "ideal gas thermometers".
