Custom Search
TORSION
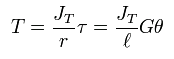
_In solid mechanics, torsion is the twisting of an object due to an applied torque, therefore is expressed in N·m or ft·lbf. In sections perpendicular to the torque axis, the resultant shear stress in this section is perpendicular to the radius.
Assumptions in theory of pure torsion
The theory of Torsion is based on the following Assumptions :
For solid shafts of uniform circular cross-section or hollow circular shafts with constant wall thickness, the torsion is:
where:
Assumptions in theory of pure torsion
The theory of Torsion is based on the following Assumptions :
- The material in the shaft is uniform throughout
- The twist along the shaft is uniform
- The shaft is of uniform circular cross section throughout
- Cross-section of the shaft, which are plane before twist remain plane after twist.
For solid shafts of uniform circular cross-section or hollow circular shafts with constant wall thickness, the torsion is:
where:
- is the maximum shear stress at the outer surface.
- JT is the torsion constant for the section. It is identical to the second moment of area Jzz for concentric tube only. For other shapes J must be determined by other means. For solid shafts the membrane analogy is useful, and for thin walled tubes of arbitrary shape the shear flow approximation is fairly good, if the section is not re-entrant. For thick walled tubes of arbitrary shape there is no simple solution, and finite element analysis (FEA) may be the best method.
- r is the distance between the rotational axis and the furthest point in the section (at the outer surface).
- ℓ is the length of the object the torque is being applied to or over.
- θ is the angle of twist in radians.
- G is the shear modulus or more commonly the modulus of rigidity and is usually given in gigapascals (GPa), lbf/in2 (psi), or lbf/ft2.
- The product JT G is called the torsional rigidity wT.
PROPERTIES

_
The shear stress at a point within a shaft is:
Note that the highest shear stress is at the point where the radius is maximum, the surface of the shaft. High stresses at the surface may be compounded by stress concentrations such as rough spots. Thus, shafts for use in high torsion are polished to a fine surface finish to reduce the maximum stress in the shaft and increase its service life.
The angle of twist can be found by using:
The shear stress at a point within a shaft is:
Note that the highest shear stress is at the point where the radius is maximum, the surface of the shaft. High stresses at the surface may be compounded by stress concentrations such as rough spots. Thus, shafts for use in high torsion are polished to a fine surface finish to reduce the maximum stress in the shaft and increase its service life.
The angle of twist can be found by using:
SAMPLE CALCULATION
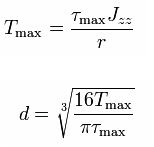
_
Calculation of the steam turbine shaft radius for a turboset:
Assumptions:
w = 2*pi*f
The torque carried by the shaft is related to the power by the following equation:
P = T*w
The angular frequency is therefore 314.16 rad/s and the torque 3.1831 x 106 N·m.
The maximal torque is:
After substitution of the polar moment of inertia the following expression is obtained:
The diameter is 0.4 m. If one adds a factor of safety of 5 and re-calculates the radius with the maximal stress equal to the yield stress/5 the result is a diameter of 69 cm, the approximate size of a turboset shaft in a nuclear power plant.
Calculation of the steam turbine shaft radius for a turboset:
Assumptions:
- Power carried by the shaft is 1000 MW; this is typical for a large nuclear power plant.
- Yield stress of the steel used to make the shaft (τyield) is: 250 x 106 N/m².
- Electricity has a frequency of 50 Hz; this is the typical frequency in Europe. In North America the frequency is 60 Hz.
w = 2*pi*f
The torque carried by the shaft is related to the power by the following equation:
P = T*w
The angular frequency is therefore 314.16 rad/s and the torque 3.1831 x 106 N·m.
The maximal torque is:
After substitution of the polar moment of inertia the following expression is obtained:
The diameter is 0.4 m. If one adds a factor of safety of 5 and re-calculates the radius with the maximal stress equal to the yield stress/5 the result is a diameter of 69 cm, the approximate size of a turboset shaft in a nuclear power plant.